|
Pondichéry |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Un centre d'appel comptait en 2001 soixante six employés. Le tableau ci-dessous donne l'évolution du nombre d'employés en fonction du rang de l'année.
On cherche à étudier l'évolution du nombre y d'employés en fonction du rang x de l'année. Une étude graphique montre qu'un ajustement affine ne convient pas.
On pose alors
1. Recopier et compléter le tableau suivant (on donnera les résultats sous forme décimale, arrondis au centième).
2. Représenter le nuage de points Un ajustement affine vous paraît-il approprié ? Justifier la réponse.
3. Déterminer, à l’aide de la calculatrice, une équation de la droite d'ajustement affine de z en x par la méthode des moindres carrés (on donnera les coefficients sous forme décimale, arrondis au centième). Tracer cette droite sur le graphique précédent.
4. En utilisant cet ajustement, à partir de quelle année peut-on prévoir que l’effectif de ce centre d'appel dépassera 900 employés ?
|
Analyse
Un exercice sur le thème de l’ajustement (séries statistiques à deux variables) avec un changement de variable finalement assez peu classique pour un sujet de BAC. Il n’en résulte cependant pas de difficulté insurmontable !
Résolution


On obtient facilement :
|
Année |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
|
Rang de l’année |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
5,12 |
7,20 |
8,40 |
10,39 |
14,03 |
15,57 |
17,69 |


A partir de ces deux séries de valeurs, on obtient le nuage de points associé (voir ci-après).
Les points sont globalement alignés
et un ajustement affine peut raisonnablement être envisagé.


A l’aide de la calculatrice, on obtient par la méthode des moindres carrés l’équation suivante de la droite de régression de z en x (les coefficients on été arrondis au centième) :
Une équation de la droite de régression de z en x obtenue par la méthode des moindres carrés (coefficients arrondis au centième) s’écrit :


équivaut à
puis
.
Il convient donc ici de résoudre l’inéquation :
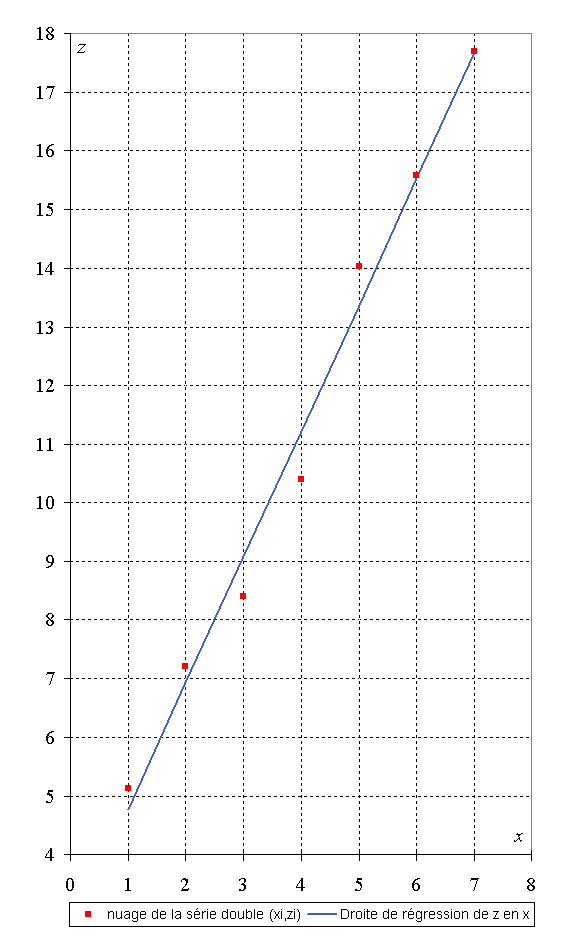
Le nuage de points
associé à la série double
et la droite de régression de z en x obtenue par la méthode des moindres carrés.
En utilisant l’ajustement obtenu à la question précédente, il vient alors :
Cette inéquation se résout comme suit :
Comme ,
on retient pour x la valeur 12.
Le rang 12 correspond à l’année : .
L’effectif du centre d’appel aura dépassé 900 employés à partir de 2012.