Les questions 1) et 2) peuvent être traitées indépendamment l’une de l’autre.   1)     On considère l’ensemble  et l’application f de E dans E définie par :                                       a)      Déterminer les antécédents par f de chacun des éléments de l’ensemble E. b)      L’application f est-elle une injection de E dans E ? (Justifier) c)      L’application f est-elle une surjection de E sur E ? (Justifier)   2)   On considère le graphe G, de sommets , tel que les successeurs de  sont respectivement . a)      Donner une représentation graphique de ce graphe. b)      On note M la matrice d’adjacence de G. On constate que . Expliquer pourquoi la première ligne de M est 0 1 0. c)      On note  la fermeture transitive de G. On rappelle que  est le graphe obtenu en conservant les sommets de G et en ajoutant, s’ils n’existent pas dans G, les arcs  lorsqu’il existe un chemin d’origine xi et d’extrémité xj dans le graphe G. Tracer une représentation géométrique de  et vérifier que la matrice d’adjacence  du graphe  est d)      Calculer les matrices booléennes  et . Vérifier que , où  représente l’addition booléenne des matrices.

 

 

La première question nécessite des connaissances de bases relatives aux applications (image, antécédent, application injective, application surjective).

La deuxième question requiert des connaissances de bases relatives aux graphes (successeur, arc, chemin, adjacence) et aux matrices booléennes.

 

 

 

 

Question 1

 

Question 1.a.

La définition de l’application f nous permet d’écrire directement :

 

• x₁ n’admet pas d’antécédent ;
• Les antécédents de x₂ par f sont x₁ et x₃ ;
• L’antécédent de x₃ par f est x₂ ;

 

 

Question 1.b.

 

L’application f n’est pas une injection de E dans E car il existe un élément de E (x₂) qui admet plus d’un antécédent par l’application f.

 

 

Question 1.c.

 

L’application f n’est pas une surjection de E sur E car il existe un élément de E (x₁) qui n’admet pas d’antécédent par l’application f.

 

 

Question 2

 

Question 2.a.

 

On a facilement :

 

 

 

 

 

 

 

 

 

 

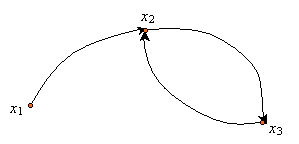
Question 2.b.

 

On a : .

 

On note classiquement m_ij le terme de la matrice M situé à l’intersection de la i‑ème ligne et de la j‑ème colonne.

 

Analyse de la première ligne de la matrice M :

 

• m₁₁ est égal à 0 car x₁ n’est pas son propre successeur (  ) ;
• m₁₂ est égal à 1 car x₂ est le successeur de x₁ (  ) ;
• m₁₃ est égal à 0 car x₃ n’est pas le successeur de x₁ (  ) 

 

 

Question 2.c.

 

A partir de la représentation graphique obtenue en 2.a., on obtient rapidement celle de la fermeture transitive de G :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

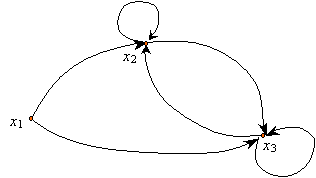
On vérifie immédiatement que l’on a :

 

 

Question 2.d.

 

On peut disposer la matrice M classiquement pour effectuer le produit :

 

 

On a donc :

 

Comme , on peut poser et calculer le produit  comme suit :

 

 

 

 

On a donc : , soit .

 

 

Il vient alors :

 

 

On a bien vérifié l’égalité : .