Etudier les branches infinies de la courbe paramétrée définie par :
Déterminer les points d’intersection de et de son asymptote.
Analyse
Il s’agit d’une étude classique d’une courbe paramétrée définie en coordonnées cartésiennes.
Dans ce qui suit, nous désignerons par la courbe représentative du graphe de
.
Résolution
Préambule
Les fonctions x et y de la variable t sont
définies sur .
On doit donc étudier les branches infinies en
,
et en
(étude à gauche et à droite).
Etude des branches infinies
Etude en
Les fonctions x et y étant rationnelles, il vient :
On a alors :
On en déduit que admet en
une branche parabolique de direction Oy,
cette branche étant orientée vers les ordonnées négatives.
Etude en
On obtient cette fois (les calculs sont similaires à ce qui vient d’être fait) :
Et :
On en déduit cette fois que admet en
une branche parabolique de direction Oy,
cette branche étant orientée vers les ordonnées positives.
Etude en
On a facilement :
Il vient alors :
Et :
On a par ailleurs :
On en déduit que lorsque t tend vers ,
admet une direction asymptotique
d’équation
.
Pour mettre en évidence une éventuelle asymptote, nous
étudions : .
Pour ,
on a :
Il vient alors :
On en déduit que lorsque t tend vers ,
admet une asymptote
d’équation :
Pour déterminer les éventuels points d’intersection de et de son asymptote
,
nous étudions : .
Pour ,
on a :
On constate que annule la fonction polynôme
.
On a alors :
On travaille sur ;
On ne prend donc pas en compte le premier facteur.
Résolvons alors : .
Il vient : puis :
et
En tenant compte du fait que et
sont solutions de
et
(on peut ainsi exprimer simplement leurs
carrés et leurs cubes), il vient :
et
Et :
et
L’asymptote et la courbe
admettent donc deux points d’intersection :
et
Résultat final
La courbe paramétrée définie par :
admet :
·
Deux branches paraboliques de
direction Oy. L’un tournée vers les ordonnées négatives ( ), l’autre tournée vers les ordonnées
positives (
) ;
·
Une asymptote d’équation
qui coupe
en :
et
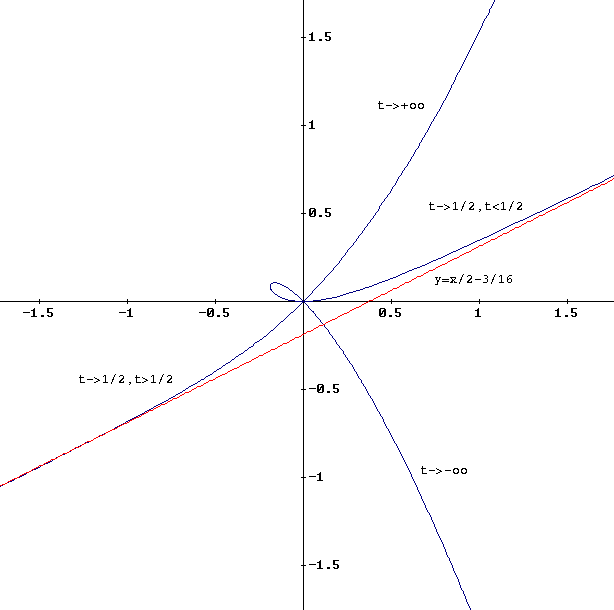
Complément
En guise de complément, nous fournissons l’allure de (en bleu) et de son asymptote (en rouge).