Il s’agit d’une courbe paramétrée définie en coordonnées cartésiennes.

Dans ce qui suit, nous désignerons par  la courbe représentative du graphe de .

On a facilement les limites en l’infini des fonctions x et y ainsi que celles du rapport.

L’annulation simultanée des dérivées de ces fonctions donne un unique point stationnaire dont on détermine facilement la nature.

 

 

 

 

Etude des branches infinies

 

Les fonctions x et y de la variable t sont définies sur . On doit donc étudier les branches infinies en  et en .

 

Les fonctions x et y étant des fonctions polynômes, il vient :

 

 

 

On a alors :

 

 

Mais par ailleurs :

 

 

On en déduit que  admet en  et en  une branche parabolique de direction la première bissectrice (d’équation  ).

 

 

Point(s) stationnaire(s)

 

On résout :

 

 

On a :

 

 

Comme  et , l’arc  admet pour unique point stationnaire le point .

 

On a facilement :

 

 

D’où : .

Les dérivées secondes étant non toutes deux nulles, on obtient ainsi les coordonnées d’un vecteur directeur de la tangente à  au point  qui est un point de rebroussement (  ). Quant à l’équation réduite de cette tangente, elle s’écrit :

 

 

Remarque : on retrouvera la valeur du coefficient directeur (  ) en calculant : .

 

Enfin, on a :

 

 

Le vecteur  étant indépendant du vecteur , le point A est ainsi un point de rebroussement de deuxième espèce (  et  ) : l’arc traverse la tangente à  en A.

 

 

 

 

 

 

 

 

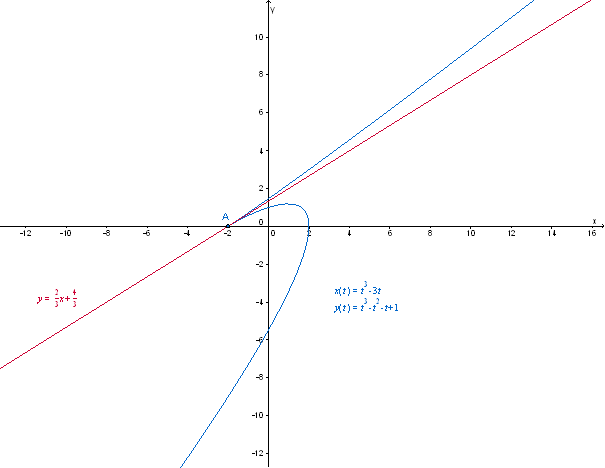
En guise de complément, nous fournissons ci-dessous une représentation graphique de  (en bleu) et de la tangente (en rouge) à  au point A.