On peut répondre en adoptant deux approches assez différentes : dénombrer le nombre de tirages et le nombre de tirages favorables ; adopter une approche plus probabiliste en s’aidant, éventuellement, d’un arbre.

 

 

 

Notons p la probabilité cherchée.

 

1^ère approche

 

Nous pouvons numéroter les boules par la pensée : R₁, R₂ et R₃ pour les rouges, V₁, V₂ et V₃ pour les vertes et, enfin, J₁, J₂ et J₃ pour les jaunes.

 

Tirer 3 boules simultanément de l’urne équivaut à les tirer individuellement et successivement sans tenir compte de l’ordre à l’issue du tirage.

 

Dans ces conditions, le nombre total N de tirages vaut :

 

 

 

Pour déterminer le nombre N_D de tirages de 3 boules de 3 couleurs différentes, on peut procéder comme suit :

• On a 9 possibilités pour la première boule ;
• Ensuite, on a 6 possibilités pour la seconde (on doit choisir une boule parmi les 6 dont la couleur est différente de la couleur de la première boule) ;
• Enfin, on a 3 possibilités pour la dernière boule.

 

Mais l’ordre n’intervenant pas, il convient de diviser  par le nombre de permutations de 3 boules, c’est à dire  :

 

 

 

Finalement :

 

 

 

 

2^ème approche

 

On peut s’aider de l’arbre suivant (nous avons fourni quelques probabilités pour fixer les idées et indiqué en gras les 6 chemins correspondant à l’événement « les 3 boules tirées sont de couleurs différentes ») :

 

 

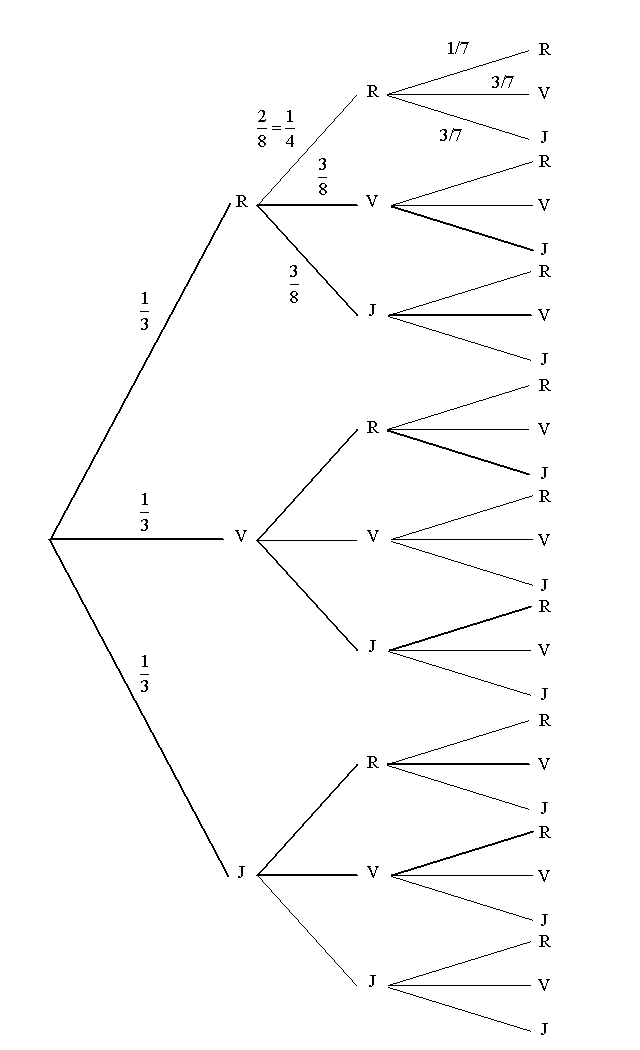
L’événement « les trois boules tirées sont de couleurs différentes » est réalisées par les 6 listes : RVJ, RJV, VRJ, VJR, JRV et JVR qui admettent pour probabilité commune :

 

 

 

Il vient alors :

 

 

 

On a ainsi retrouvé le résultat obtenu précédemment.