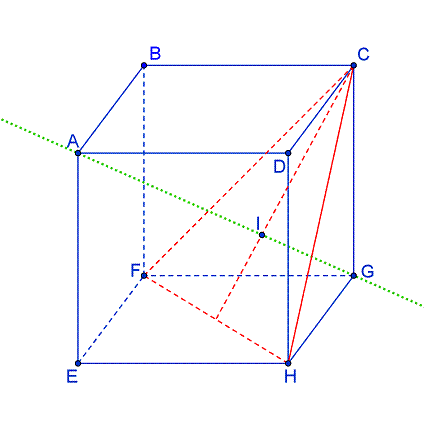
On considère un cube ABCDEFGH d’arête a.
On note I l’isobarycentre du triangle CFH.
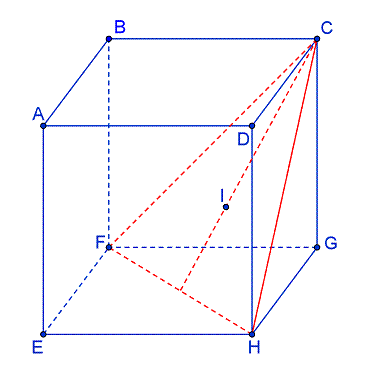
1. Montrer que le triangle CFH est équilatéral.
2. Prouver que les points A, G et I
appartiennent au plan médiateur de et au plan
médiateur de
.
3. En déduire que la droite est orthogonale
au plan
et qu’elle
passe par I.
(D’après BAC E 1989)
Analyse
Un exercice sur l’orthogonalité dans l’espace qui met l’accent sur la notion de plan médiateur. Seule la troisième question requiert un peu de précision.
Résolution
1. Les côtés du triangle CFH sont des diagonales de faces du cube. Toutes
les faces du cube sont des carrés de côté a et de diagonale .
Il vient donc immédiatement :
Le triangle CFH est équilatéral.
2. Rappelons que le plan médiateur d’un segment dans l’espace est l’ensemble des points équidistants des extrémités de ce segment.
est une diagonale du carré ADCB. On a
donc :
.
est une diagonale du carré ADHE. On a
donc :
.
Comme ,
le point A appartient au plan médiateur du segment
.
et
sont deux côtés du carré DCGH. On a donc
.
Comme ,
le point G appartient au plan médiateur du segment
.
Enfin, le point I étant
l’isobarycentre du triangle CFH qui est équilatéral, il en est le point
d’intersection des médiatrices. En particulier, I appartient à la médiatrice du
segment dans le plan
.
On a donc
et le point I appartient au plan médiateur du
segment
.
En raisonnant de façon similaire
avec le segment ,
on montre que les points A, G et I appartiennent au plan médiateur de ce
segment.
Les
points A, G et I appartiennent aux plans médiateurs des segments et
.
3. Notons et
les plans médiateurs des segments
et
respectivement.
Ils admettent pour vecteurs
normaux et
respectivement. Ces vecteurs n’étant pas
colinéaires, les deux plans
et
se coupent suivant une droite. Comme les
points A, G et I appartiennent à l’intersection de
et
(cf. la question précédente), on en déduit
immédiatement que la droite
passe par le point I.
Le plan passe par le milieu du segment
et est perpendiculaire à la droite
.
Toute droite de
est donc orthogonale à la droite
.
A et G étant deux points du plan ,
on déduit de ce qui précède que la droite
est orthogonale à la droite
.
En raisonnant de façon similaire
avec le plan et le segment
,
on établit que la droite
est orthogonale à la droite
.
La droite étant orthogonale aux deux droites sécantes
et
,
on en déduit immédiatement qu’elle est perpendiculaire au plan
.
En définitive :
La
droite est perpendiculaire au plan
et passe par le point I de ce plan.