Deux questions dont les réponses pourraient figurer dans un cours !

On répond facilement à la première en revenant à la définition d’une fonction convexe sur un intervalle.

On peut assez facilement avoir l’intuition qu’une combinaison linéaire quelconque de deux fonctions convexes sur un intervalle n’est pas convexe sur cet intervalle. Il convient alors de préciser un peu les choses …

 

 

 

 

Pour chacune de deux questions, nous considérons f et g deux fonctions convexes sur un intervalle I.

 

Question 1.

 

Soit x et y deux réels de l’intervalle I et t un réel de l’intervalle .

 

Les fonctions f et g étant convexes sur I, on a :

 

 

 

En additionnant ces deux inégalités membre à membre, il vient :

 

 

 

Soit :

 

 

 

Ainsi, la fonction  est convexe sur I.

 

 

 

Question 2.

 

Une démarche similaire à celle que nous avons proposée à la question précédente nous permet facilement d’établir :

 

·        Pour tout couple  de réels positifs, la fonction  est convexe.

·        Pour tout couple  de réels négatifs, la fonction  est concave.

 

En revanche, lorsque les réels α et β sont non nuls et de signes contraires, on ne peut conclure.

 

Considérons par exemple les fonctions carré et cube qui sont convexes sur .

Leur différence est la fonction  (cf. la représentation graphique ci-dessous) qui est :

 

·        Concave sur l’intervalle  ;

·        Convexe sur .

 

 

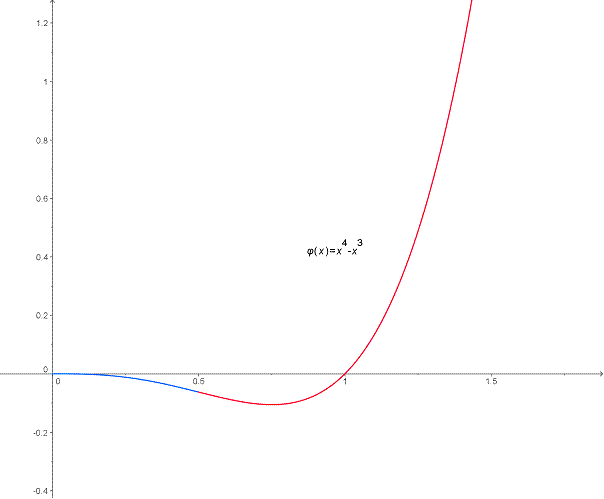
Représentation graphique de la fonction  définie sur .

La branche bleue correspond à , intervalle sur lequel f est concave.

La branche rouge correspond à , intervalle sur lequel f est convexe.

 

 

Ainsi, on ne peut rien dire d’une combinaison linéaire quelconque de deux fonctions convexes sur un intervalle donné (en considérant la fonction ci-dessus sur l’intervalle , on constate que la différence de deux fonctions convexes sur un intervalle donné peut être une fonction concave sur cet intervalle).