On utilise le fait que l’orthocentre est le point de concours des trois hauteurs. En fait, on utilise seulement le fait que H appartient à deux d’entre elles, cette appartenance s’exprimant, pour une hauteur donnée, sous la forme de l’orthogonalité de deux vecteurs.

 

 

 

 

En guise de préambule, précisons que nous noterons classiquement a, b et c les affixes respectives des points A, B et C.

 

 

Le point H étant un point de la hauteur issue de A du triangle ABC, on a :

 

 

Comme , on en déduit immédiatement que le complexe  est un imaginaire pur. On a donc :

 

 

Soit :

 

 

D’où :

 

 

Avec les valeurs de l’énoncé, on obtient :  et, de fait, . D’où : .

 

L’équation  se récrit alors :

 

 

Le point H étant également un point de la hauteur issue de B du triangle ABC, on a :

 

 

Comme ci-dessus, on en tire alors :

 

 

Egalité qui donne :

 

 

Numériquement, on obtient :

 

 

Soit, après simplification :

 

 

Finalement, on dispose du système :

 

 

La combinaison  donne :

 

 

Soit :

 

 

Or :

 

 

On a donc : , soit : .

 

 

 

 

 

 

 

 

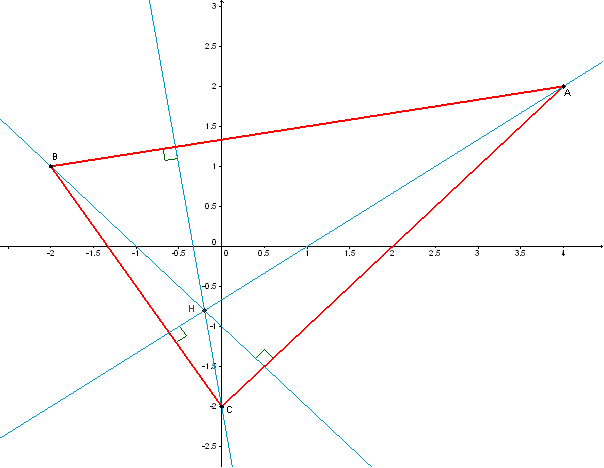
A titre de complément, nous fournissons une représentation graphique du triangle ABC, de ses trois hauteurs et de leur point de concours : H.