Deux asymptotes à mettre en évidence en appliquant le cours. La présence de la racine carrée dans l’expression de la fonction f requiert l’usage d’expressions conjuguées.

 

 

 

1.       existe si, et seulement si,  est supérieur ou égal à 0.

On résout donc : .

Le discriminant se calcule facilement : . Comme il est strictement négatif, la quantité  garde un signe constant qui est celui du coefficient de . Comme celui-ci vaut 4, on en déduit : .

On en conclut finalement que  existe pour tout x réel.

 

 

 

2.      Etudions maintenant la limite en  de .

 Commençons par travailler en .

On a : .

La fonction f est la composée de la fonction  et de la fonction racine carrée.

On a facilement :  et .

On en déduit alors : .

On a par ailleurs : .

Pour le calcul de , nous sommes donc confrontés à une forme indéterminée du type «  ».

Afin de lever cette indétermination, nous allons travailler avec l’expression conjuguée de . Pour tout réel x (on vérifiera que la quantité  ne peut être nulle), on a en effet :

 

 

 

Comme  on a :

 

 

D’où, finalement : .

 

 Travaillons maintenant en .

On a :  et .

Pour le calcul de , nous sommes donc encore confrontés à une forme indéterminée du type «  ».

On procède comme précédemment et on obtient cette fois :

 

 

 

Comme  on a, ici encore :

 

 

D’où, finalement : .

 

 

 

3.      Pour étudier la position de C_f par rapport à , nous devons étudier le signe de la différence : .

D’après la première question, on a déjà : .

Si , on a immédiatement .

Si , les quantités  et  sont toutes deux strictement positives et on peut comparer leurs carrés. La différence  a été calculée à la question 2 et est strictement positive. On en déduit : .

Finalement, pour tout x réel, on a : .

 

 

On démontre de façon similaire que :

 

 

 

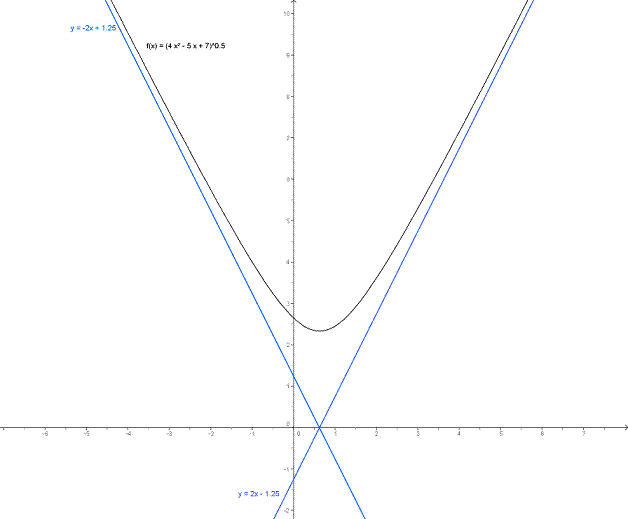
A titre de complément, nous fournissons ci-après une représentation graphique de la fonction f (en noir) et de ses deux asymptotes (en bleu).